Auto Encoder 调研总结
youngyhli
Part I
AutoEncoder 和 PCA 有着直接的联系
AutoEncoder v.s. PCA
- 使用线性激活函数的AE可以近似PCA。数学上来说,最小化重建误差的PCA等价于单层线性AE
- AE把PCA扩展到了非线性空间,换句话说,AE是PCA的非线性拓展
因此,AE应该有着和PCA相似的性质:
- 权值捆绑(encoder和对应的decoder之间)
- 权值正交 (每一个权值向量之间互相独立)
- 特征无关(encoder生成的特征是不相关的)
- 单位范数(Unit Norm)(同一层的权值有单位范数)
然而,大多数教程中的AE实现并没有以上性质, 这使得它们不是最优的。因此,融入这些性质来实现一个好的AE蛮重要的,为了做到这,我们需要:
- 加入正则化:正交和单位范数的限制条件其实是一种正则化。此外,权值捆绑,几乎减少了一半的参数量,也是一种正则化
- 强调梯度爆炸和梯度消失:单位范数的限制防止权重变大,因此解决了梯度爆炸的问题。此外,因为正交这一限制条件,只有重要的(充满信息的)权值是非零的。因此,大量的信息在BP的时候通过这些权重进行传递从而避免梯度消失
- 有更小的网络:如果没有正交条件的限制,encoder会有大量冗余的参数和特征。为了抵消这种冗余,encoder的size增大了。另一方面,正交性保证编码的特征有其独特的信息——独立于其他的特征。这减少了冗余从而我们可以在更小的encoder上有类似的信息。
With a smaller network, we bring Autoencoder closer to Edge Computing.
这部分展示了:
- PCA和AutoEncoder之间架构的相似性
- 传统Autoencoder的次优性
PCA和AutoEncoder架构之间的相似性:线性单层AE v.s. PCA
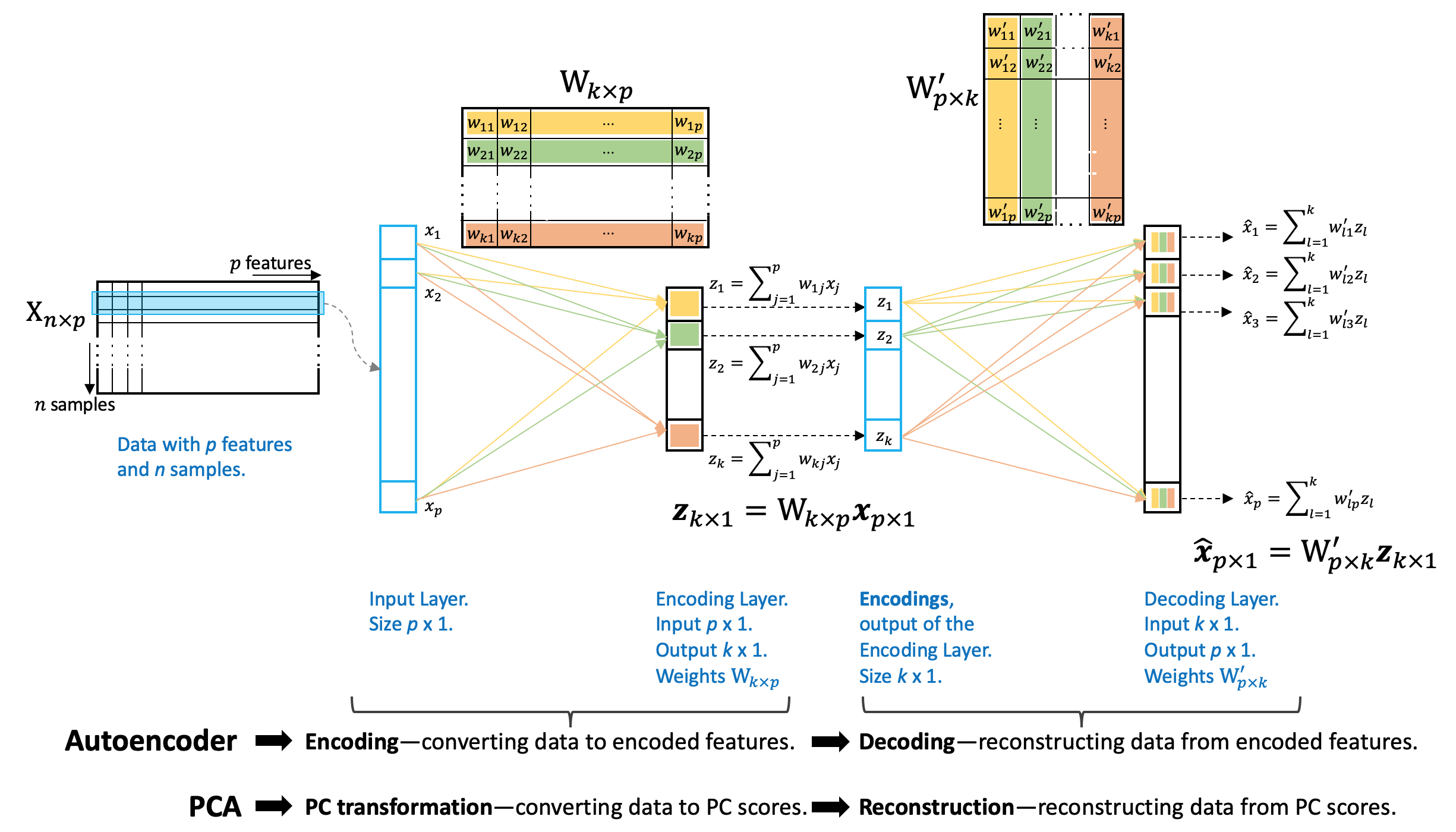
众多PCA算法中,有一种是通过最小化重建误差实现的,从这种算法出发可以很清晰地看到PCA和AE之间的相似性
如图所示,
- Encoding的过程和PC变换的过程很像(PC变换把原始数据映射到主成分上来生成正交的特征,a.k.a, PC scores)
- 同样地,Decoding的过程和从PC scores重建数据很相似
- 它们的参数都是通过最小化重建误差来估计的
【更多细节参见原文】
Part II
这部分定义并实现加了正则项约束的AutoEncoder
从Part I我们知道传统的AE有PCA的相似架构但却没有它的优良性质,而且我们明白了融合PCA的性质会带来巨大的好处:诸如解决梯度消失、爆炸,过拟合等问题。基于此,我们想要AE继承的性质有:1. Tied Weights;2. Orthogonal Weights; 3. Uncorrelated Features; 4. Unit Norm. 在这部分,我们将:
- 实现自定义的层和约束条件来融合它们
- 演示它们是怎么起作用的,以及它们带来的重建误差上的改进
Note: regularization techniques, such as, dropout, are popularly used. But without a well-posed model, these approaches take longer to optimize.
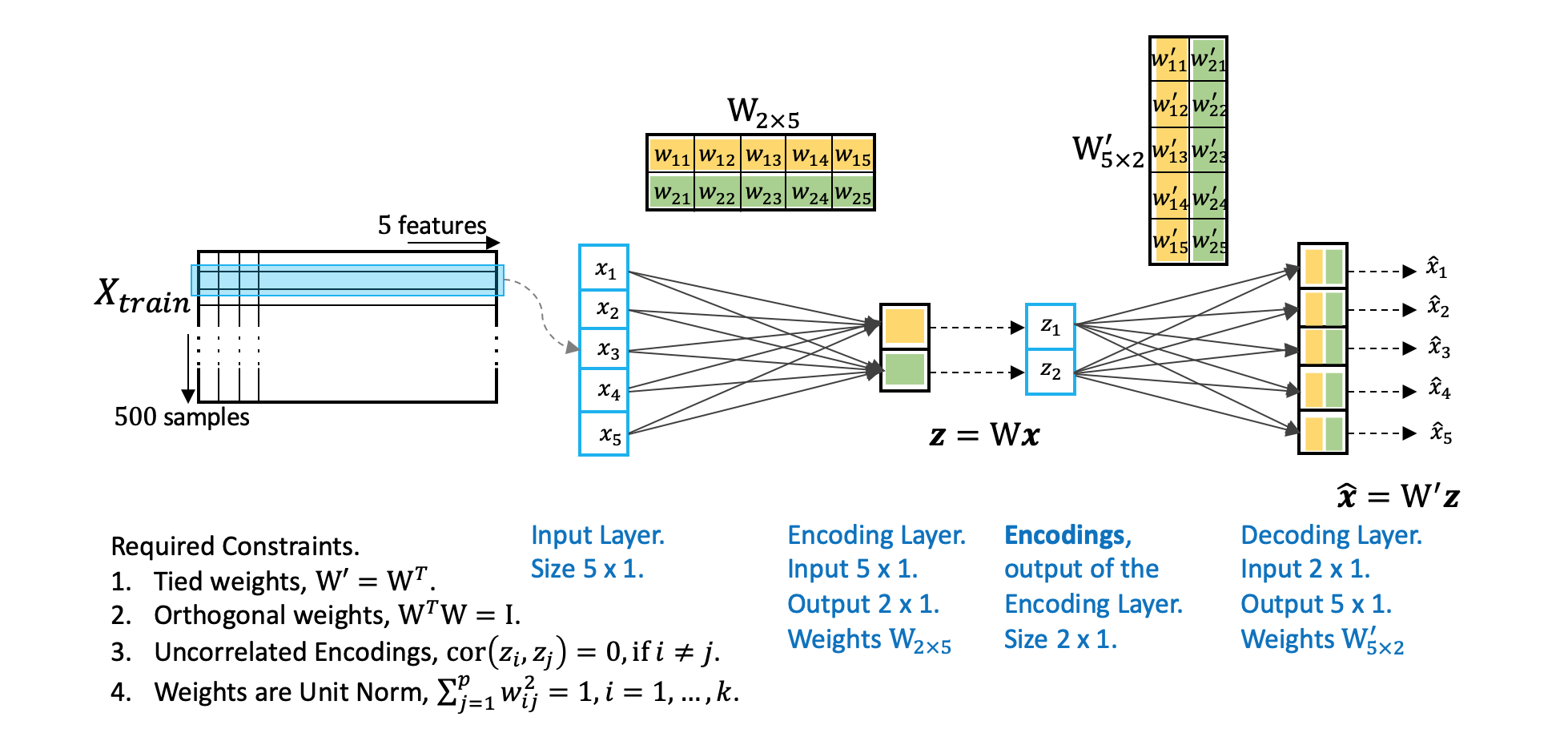
关键点
Tied Weights
- 在权值捆绑层,DenseTied, Encoder和Decoder的偏置会不同
- 如果要使得所有对应的权值都是相等的,可以设置
use_bias=False
Weight Orthogonality
- 使用
kernel_regularizer来给对应层的权值添加约束条件 - 对于Encoder,设置
axis=0,而对于Decoder,设置axis=1
Uncorrelated Encoded features
- 使用
activity_regularizer来给输出特征层(Encoder最后一层)添加约束条件(约束编码器得到的特征的非对角元的协方差为0)。 - 需要说明的是,这个约束并不强,它并没有要求协方差矩阵非对角元严格为0
- 可以探索其他的实现方式
Unit Norm
- 单位范数对于Encoder和Decoder来说是在不同的轴(axes)的
- 和权值正交相似,这也是对Encoder设置
axis=0,对Decoder设置axis=1